Activité « La force d’interaction gravitationnelle »
1 Introduction
Précédemment, grâce à la vidéo « Newton et la gravitation » et au texte tiré du site de JP luminet, nous avons vu que Newton pressentait deux paramètres pertinents dans l’étude de la chute d’un corps : Voir les deux extraits suivants :
- « … Et si la matière attire ainsi la matière, cela doit être en proportion de sa quantité1 … »
- « … le pouvoir de la gravité (qui faisait tomber la pomme de l’arbre vers le sol) ne se limitait pas à une certaine distance de la surface terrestre, mais qu’il devait s’étendre beaucoup plus loin … »
2 Document 1 « Philosophiae naturalis principia mathematica » d’Isaac Newton
« Principes mathématiques de la philosophie naturelle »,est l’œuvre maîtresse d’Isaac Newton, publiée à Londres en 1687. C’est la troisième édition latine, de 1726, dont le texte aura été enrichi une dernière fois par Newton, qui est généralement considérée comme référence.
2.1 Extrait 1 :
- « Tous les corps gravitent vers chaque planète, et sur la même planète, leurs poids, à égale distance du centre, sont proportionnels à la quantité de matière que chacun d’eux [corps et planète] contient »
2.2 Extrait 2 :
- Deux sphères … s’attirent réciproquement avec des forces qui sont en raison renversée 2 du carré des distances de leurs centres.«
- Montrons la cohérence de ces extraits 1 et 2 avec les extraits rappelés en introduction : Quels sont les deux paramètres cités ?
Prendre le temps de la réflexion puis … Correction de la question 1
3 Expression de la valeur de la force d’interaction gravitationnelle
Les travaux de Newton ont permis d’exprimer la valeur commune des forces de gravitation \(\overrightarrow{F_{A/B}}\) et \(\overrightarrow{F_{B/A}}\).
- Pour deux corps A et B :
- de masses 1 \(m_{A}\) et \(m_{B}\) exprimées en kg.
- dont le centre de gravité \(G_{A}\) et \(G_{B}\) sont distants d’une distance d exprimée en m.
- avec G, constante appelée « constante de gravitation universelle » : G = \(6,67 \times 10^{-11}\) \(N.m^{2}.kg^{-2}\)
Parmi les 4 expressions suivantes (A), (B), (C), ou (D), laquelle est cohérente avec les informations précédentes et constitue donc l’expression de la valeur de la force d’interaction gravitationnelle ?
\begin{align} F_{A/B} = G.m_{A}.m_{B}.d^{2} \hspace{0.5cm} (A) \end{align} \begin{align} F_{A/B} = G.\frac{m_{A}.m_{B}}{d^{}} \hspace{0.5cm}(B) \end{align} \begin{align} F_{A/B} = G.\frac{m_{A}.m_{B}}{d^{2}} \hspace{0.5cm} (C) \end{align} \begin{align} F_{A/B} = G.\frac{d^{2}}{m_{A}.m_{B}} \hspace{0.5cm} (D) \end{align}Prendre le temps de la réflexion puis … Correction de la question 2
On pourra utiliser la simulation illustrée plus bas pour éprouver la pertinence des paramètres

4 « Cas de la Lune, satellite naturel de la Terre »
La Lune est un satellite naturel de la Terre qui gravite autour d’elle car la Terre et la Lune exercent mutuellement l’une sur l’autre une attraction gravitationnelle.


4.1 « Représentation et données »
La Terre est représentée par le point T et la Lune par le point L.
- Masse de la Terre \(M_{T}\) = \(5,97 \times 10^{24}\) kg
- Masse de la Lune \(M_{L}\) = \(7,35 \times 10^{22}\) kg
- Distance entre T et L : d = \(3,84 \times 10^{5}\) km
- Échelle du vecteur force : 1 cm représente \(1,0 \times 10^{20}\) N
- Calculer la valeur \(F_{Terre/Lune}\) de la force \(\overrightarrow{F_{Terre/Lune}}\).
Prendre le temps de la réflexion puis … Correction de la question 3
- La force \(\overrightarrow{F_{Terre/Lune}}\) est-elle représentée par \(\overrightarrow{F_{1}}\) ou \(\overrightarrow{F_{2}}\) ?
- La force \(\overrightarrow{F_{Lune/Terre}}\) est-elle représentée par \(\overrightarrow{F_{1}}\) ou \(\overrightarrow{F_{2}}\) ?
Prendre le temps de la réflexion puis … Correction de la question 4
4.2 Document 2 « Principe des actions réciproques »
Isaac Newton énonce aussi un des grands principes de la physique appelé « principe des actions réciproques » ou « principe de l’action et réaction »
« Tout système A exerçant une force sur un système B subit, de la part du système B une force de même direction, de même valeur mais de sens contraire »
Newton étend ce principe aussi bien à des actions de contact qu’à des actions à distance.
- Pourquoi peut-on dire, en comparant \(\overrightarrow{F_{Terre/Lune}}\) et \(\overrightarrow{F_{Lune/Terre}}\), que l’interaction gravitationnelle Terre-Lune est une illustration du principe des actions réciproques ?
Prendre le temps de la réflexion puis … Correction de la question 5
4.3 Expression vectorielle d’une force de gravitation
Si, dans la représentation de la question 4, sur la droite (TL), on plaçait un vecteur unitaire 3 \(\overrightarrow{u_{1}}\) dirigé dans le sens de L vers T (voir schéma précédent), on pourrait écrire :
\begin{align} \overrightarrow{F_{Terre/Lune}} = G.\frac{M_{L}.M_{T}}{d^{2}}. \overrightarrow{u_{1}} \end{align}Si, dans la représentation de la question 4, sur la droite (TL), on plaçait un vecteur unitaire \(\overrightarrow{u_{2}}\) dirigé dans le sens de T vers L (voir schéma précédent), on pourrait écrire :
\begin{align} \overrightarrow{F_{Lune/Terre}} = G.\frac{M_{L}.M_{T}}{d^{2}}. \overrightarrow{u_{2}} \end{align}- Quelle est l’expression correcte si on veut \(\overrightarrow{F_{Lune/Terre}}\) en fonction de \(\overrightarrow{u_{1}}\) ? (Aide : Bas de page 198)
Prendre le temps de la réflexion puis … Correction de la question 6
4.4 Simulation de l’interaction gravitationnelle Terre-Lune :
Lien de l’animation « Gravité et orbites » Menu « À l’échelle »
- Choisir l’interaction Terre-Lune

- La période sidérale \(T_{Lune}\) est l’intervalle de temps qui s’écoule en moyenne entre deux passages de la Lune dans une même direction par rapport aux étoiles. Évaluer la période sidérale de la Lune.
Prendre le temps de la réflexion puis … Correction de la question 7
- Quand la Lune est dans son mouvement autour de la Terre, mettre l’animation au ralenti (menu de gauche en bas) puis supprimer brutalement la gravité. Définir alors le mouvement de la Lune.
Prendre le temps de la réflexion puis … Correction de la question 8
4.5 Autres vidéo puis animation
- Visualualiser, jusqu’à 1’14, le début de la vidéo « La Gravitation sur le site du CEA »
- « Canon de Newton » pour revenir sur l’influence de la vitesse INITIALE d’un corps lors de sa chute.
5 Éléments de correction
5.1 Correction de la question 1
Les deux paramètres cités sont
- les masses \(m_{a}\) et \(m_{B}\) des deux corps A et B en présence.
- la distance d entre les centres de gravité de A et B.
5.2 Correction de la question 2
Dans l’expression \(F_{A/B} = G.\frac{m_{A}.m_{B}}{d^{2}}\)
On retrouve
- pour deux corps A et B :
- les masses \(m_{A}\) et \(m_{B}\) exprimées en kg, au numérateur de l’expression (1) : la valeur de la force gravitationnelle \(F_{A/B}\) (= \(F_{B/A}\)) est bien proportionnelle aux masses \(m_{A}\) et \(m_{B}\).
- la distance d (exprimée en m) entre les centres de gravité \(G_{A}\) et \(G_{B}\) de A et B, avec \(d^{2}\) au dénominateur de l’expression (1) : la valeur de la force gravitationnelle \(F_{A/B}\) (= \(F_{B/A}\)) est bien inversement proportionnelle au carré de la distance d entre les centres de gravité de A et B.
5.3 Correction de la question 3
\(F_{Terre/Lune} = F_{Lune/Terre} = G \times \frac{M_{T} \times M_{L}}{d^{2}}\)
- Masse de la Terre \(M_{T}\) = \(5,97 \times 10^{24}\) kg
- Masse de la Lune \(M_{L}\) = \(7,35 \times 10^{22}\) kg
- Distance entre T et L : d = \(3,84 \times 10^{5}\) km = \(3,84 \times 10^{8}\) m. Ne pas oublier de convertir d en mètres !
\(F_{Terre/Lune} = F_{Lune/Terre} = 6,67 \times 10^{-11} \times \frac{5,97 \times 10^{24} \times 7,35 \times 10^{22}}{(3,84 \times 10^{8})^{2}}\) = \(1,98 \times 10^{20}\) N.
5.4 Correction de la question 4


- La force \(\overrightarrow{F_{Terre/Lune}}\) est représentée par \(\overrightarrow{F_{2}}\).
- La force \(\overrightarrow{F_{Lune/Terre}}\) est-elle représentée par \(\overrightarrow{F_{1}}\).
- Nous constatons que la valeur de la force de gravitation
\(F_{Terre/Lune}\) (\(= F_{Lune/Terre}\)) est très proche de \(2,0 \times 10^{20}\) N.
- L’échelle proposée est 1 cm pour \(1,0 \times 10^{20}\) N
- Les vecteurs-forces auront donc une longueur de 2 cm pour représenter \(2,0 \times 10^{20}\) N
5.5 Correction de la question 5
On a \(\overrightarrow{F_{Terre/Lune}}\) = - \(\overrightarrow{F_{Lune/Terre}}\), ce qui illustre le principe des actions réciproques :
Les forces \(\overrightarrow{F_{Terre/Lune}}\) et \(\overrightarrow{F_{Lune/Terre}}\) ont :
- même direction
- sens contraires
- même valeur
NB : Il s’agit ici d’une interaction à distance
5.6 Correction de la question 6

\(\overrightarrow{F_{Lune/Terre}} = G.\frac{m_{A}.m_{B}}{d^{2}}. \overrightarrow{u_{2}} = - G.\frac{m_{A}.m_{B}}{d^{2}}. \overrightarrow{u_{1}}\)
5.7 Correction de la question 7
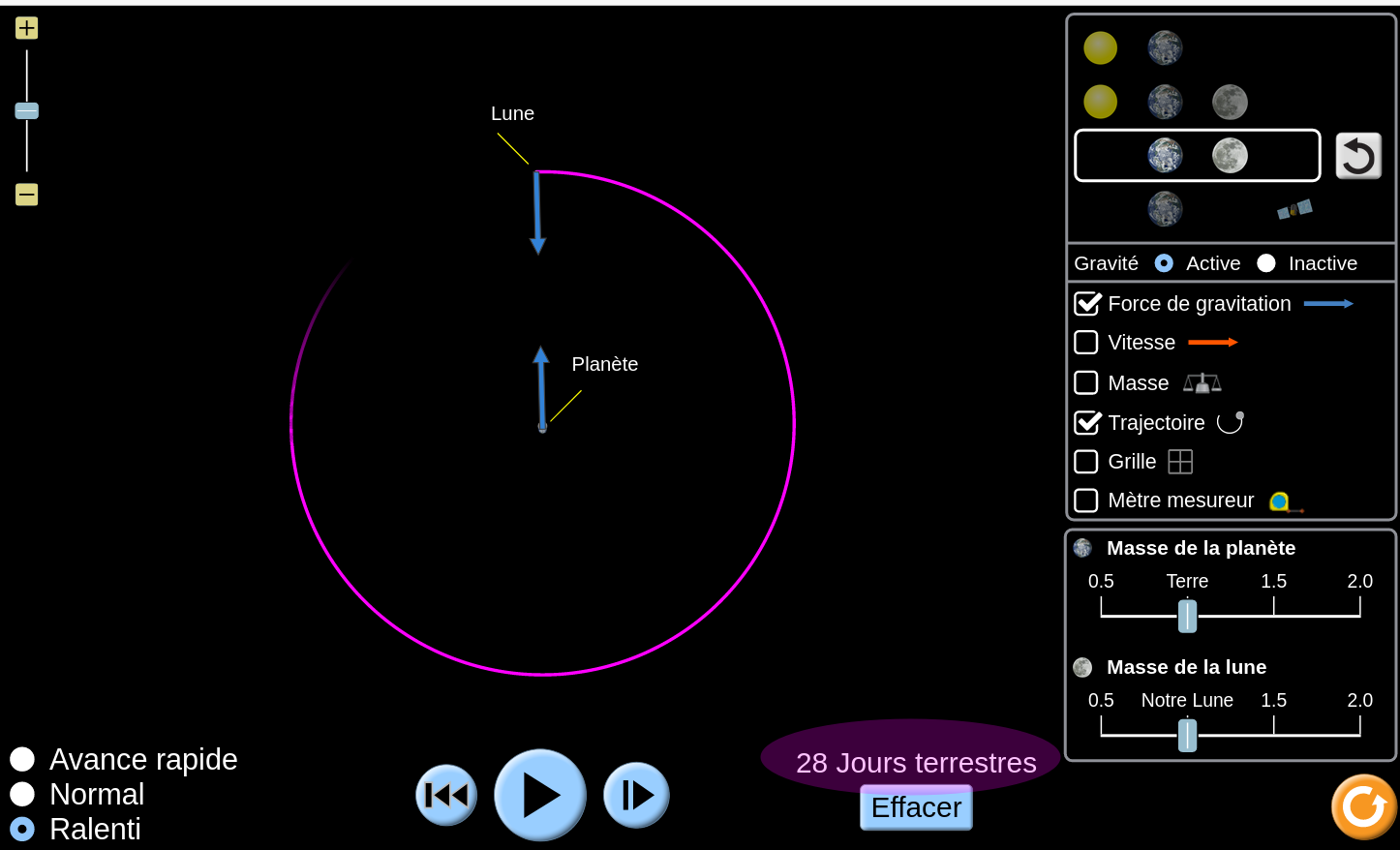
- La période sidérale de la Lune est égale à environ 28 jours terrestres soit un mois.
Plus précisément : 27,32 jours. (source : http://craq-astro.ca/phy1971/chap9/chap9b.html)

Animation Geogebra :
5.8 Correction de la question 8

- Quand, dans l’animation, la Lune étant dans son mouvement autour de la Terre, on supprime brutalement la gravité alors la Lune prend un mouvement rectiligne uniforme.
- Ce résultat, si on annule effectivement toute source de force de gravitation (pas seulement celle exercée par la Terre …) est une illustration du principe d’inertie ou première loi de Newton :
- Un corps ne subissant aucune force (ou un système de forces dont la résultante est nulle) reste
- immobile (s’il l’était initialement)
- en mouvement rectiligne uniforme.
NB : Le principe ne vaut que pour des observateurs placés dans un référentiel approprié (« référentiel galiléen »).
