"LANCER DE POIDS"

Le lancer de poids
- Nous étudierons le mouvement dans le repère cartésien (O ;
\(\overrightarrow{i}\), \(\overrightarrow{j}\), \(\overrightarrow{k}\))
avec
- \(\overrightarrow{i}\) orientant \(Ox\)
- \(\overrightarrow{j}\) orientant \(Oy\)
- \(\overrightarrow{k}\) orientant \(Oz\), vertical, ascendant.
Dans ce repère, le champ de pesanteur \(\overrightarrow{g}\), vertical descendant, a pour coordonnées :
\(\overrightarrow{g} \begin{bmatrix}0 \\ 0 \\ -g \end{bmatrix}\)
Conditions initiales
- À t = 0, le poids est à une hauteur z = h : \(\overrightarrow{OG_{o}} \begin{bmatrix}x = 0 \\ y = 0 \\ z = h = 2 \end{bmatrix}\)
- À t = 0, le poids est lancé à une vitesse initiale \(\overrightarrow{v_{o}} \begin{bmatrix}v_{x0} = v_{0}cos \alpha \\ v_{yO} = 0 \\ v_{z0} = v_{0}sin \alpha \end{bmatrix}\)
Étude mécanique d'un lancer de poids
Choix du système
Le choix du système se porte bien sûr sur l'objet "poids".
Référentiel
Nous travaillerons dans le référentiel terrestre assimilable à un référentiel galiléen.
Listes de force(s). Modèle de la chute libre
- Nous utiliserons le modèle de la chute libre où seule l'action du poids \(\overrightarrow{P}\) est prise en compte. Nous négligerons donc les actions dues à l'air (Poussée d'Archimède, frottements dus à l'air négligées)
- Un corps est en chute libre quand il n'est soumis qu'à l'action de son poids \(\overrightarrow{P}\).
Loi de Newton
- La situation n'est pas dans le champ d'application de la première loi de Newton puisque le système n'est ni isolé, ni pseudo-isolé.
- 2ème loi de Newton : \(\Sigma \overrightarrow{f} = \frac{d \overrightarrow{p}}{dt}\)
- Ici, dans le modèle de la chute libre, \(\Sigma \overrightarrow{f}\) se limite à \(\overrightarrow{P}\).
- \(\Sigma \overrightarrow{f} = \overrightarrow{P} = \frac{d \overrightarrow{p}}{dt} = \frac{d(m. \overrightarrow{v})}{dt}\).
- Ne pas confondre le vecteur poids \(\overrightarrow{P}\) et le vecteur quantité de mouvement \(\overrightarrow{p}\)
- Le système objet "Poids" garde sa masse m constante au cours de sa chute, on peut écrire :
\(\overrightarrow{P} = \frac{d(m. \overrightarrow{v})}{dt} = m \frac{d \overrightarrow{v}}{dt} = m. \overrightarrow{a}\)
puisque, par définition, l'accélération \(\overrightarrow{a} = \frac{d \overrightarrow{v}}{dt}\)
- On a donc, \(\overrightarrow{P} = m. \overrightarrow{g} = m. \overrightarrow{a}\)
- soit donc, plus simplement, \(\overrightarrow{a} = \overrightarrow{g}\)
- Or, le champ de pesanteur peut-être considéré comme constant dans un domaine incluant largement la trajectoire du système-"poids". Voir http://rene.souty.free.fr/spip.php?article81
- On a donc, puisque que \(\overrightarrow{a} = \overrightarrow{g}\), une accélération constante, le mouvement du "poids" est donc uniformément varié.
- En valeur, a = g, on en déduit que g est homogène a une accélération et peut être exprimé en \(m.s^{-2}\).
Vecteur accélération \(\overrightarrow{a}\)
\(\overrightarrow{a} = \overrightarrow{g}\) donc \(\overrightarrow{a}\) a les mêmes coordonnées que \(\overrightarrow{g}\) dans le repère cartésien décrit plus haut.
\(\overrightarrow{a} \begin{bmatrix}a_{x} = 0 \hspace{0.5 cm}(1) \\ a_{y} = 0 \hspace{0.5 cm} (2) \\ a_{z} = -g \hspace{0.5 cm} (3) \end{bmatrix}\)
Vecteur vitesse \(\overrightarrow{v}\)
\(\overrightarrow{a} \begin{bmatrix}a_{x} = \frac{dv_{x}}{dt}= 0 \\ a_{y} = \frac{dv_{y}}{dt} = 0 \\ a_{z} = \frac{dv_{z}}{dt}= -g \end{bmatrix}\)
Par recherche de primitives, on peut écrire
\(\overrightarrow{v} \begin{bmatrix}v_{x} = cste = v_{O}cos \alpha \hspace{0.5 cm}(4) \\ v_{y} = cste = 0 \hspace{0.5 cm} (5)\\ v_{z} = -gt + cste = -gt + v_{0}sin \alpha \hspace{0.5 cm} (6) \end{bmatrix}\)
Vecteur position \(\overrightarrow{OG}\)
\(\overrightarrow{v} \begin{bmatrix}v_{x} = \frac{dx}{dt} = v_{O}cos \alpha \\ v_{y} = \frac{dy}{dt} = 0 \\ v_{z} = \frac{dy}{dt} = -gt + v_{0}sin \alpha \end{bmatrix}\)
Par recherche de primitives, on peut écrire
\(\overrightarrow{OG} \begin{bmatrix}x = v_{O}cos \alpha t + cste = v_{O}cos \alpha t \hspace{0.5 cm} (7) \\ y = cste = 0 \hspace{0.5 cm}(8) \\ z = -\frac{1}{2} gt^{2} + v_{0}sin \alpha t + cste = -\frac{1}{2} gt^{2} + v_{0}sin \alpha t + h \hspace{0.5 cm}(9) \end{bmatrix}\)
- Les équations f(t) précédentes sont des équations horaires.
- L'équation (8) y = 0 montre que le mouvement du "poids" est plan. Il est donc possible de ne garder qu'un repère cartésien à deux dimensions (O ; \(\overrightarrow{i}\), \(\overrightarrow{j}\))
- L'équation (4) (et sa conséquence (7)) montrent que le mouvement projeté sur [Ox) est un mouvement uniforme.
Équation de trajectoire
- D'après (7) \(t = \frac{x}{v_{0}cos \alpha}\)
- Dans (9) \(z = -\frac{1}{2} gt^{2} + v_{0}sin \alpha t + h\)
- \(z = -\frac{1}{2} g(\frac{x}{v_{0}cos \alpha})^{2} + v_{0}sin \alpha \times \frac{x}{v_{0}cos \alpha} + h\)
- \(z = -\frac{g}{2v_{0}^{2}cos^{2}\alpha}x^{2} + xtan \alpha + h \hspace{0.5cm}(10)\)
- (10) est une équation z = f(x), équation de trajectoire du type ”\(z = ax^{2} + bx + c\)” : arc de parabole
Quel point C le "poids" atteindra-t-il au sol ? (c'est à dire "portée du poids" ?)
- Pour atteindre cet objectif
- Quelle particularité présente le point C, point du sol atteint par le "poids" ? \(y_{C}\) = ?
- À reporter dans l'équation de trajectoire puis résoudre l'équation de second degré de type "\(ax^{2} + bx + c = 0\)" dont l'une des solutions est \(x_{C}\)
- La particularité de C est d'être au sol d'où \(z_{C}\) = 0.
- Pour tout point de la trajectoire : \(z = -\dfrac{g}{2v_{o}^{2}cos^{2}\alpha}x^{2} + xtan\alpha\) + h
- Pour C : \(z_{C} = 0 = -\dfrac{g}{2v_{o}^{2}cos^{2}\alpha}x^{2} + xtan\alpha + h\)
- Prenons, par exemple, \(\alpha = 35^{o}\), \(v_{0}\) = 14 \(m.s^{-1}\), h = 2 m.
- On obtient l'équation de second degré : \(z_{C}= -\dfrac{9,81}{2 \times 14^{2}cos^{2}(35)}x_{C}^{2} + x_{C}tan(35) + 2 = 0\)
- \(z_{C} = -3.73 \times 10^{-2} x_{C}^{2} + 0,700 \times x_{C} + 2 = 0\)
- L'équation du second degré précédente du type \(ax^{2} +bx + c = 0\) a deux solutions : Voir, par exemple, Résolution d'équation du 2d degré en ligne avec a = -0,0373 ; b = 0,700 et c = 2.
- Ces solutions sont 21,3 et 2,52. La seule solution physiquement acceptable est bien sûr \(x_{C}\) = 21,3 m.
- Grâce à un simulateur comme celui de de W. Fendt et Y. Weiss (Lien sur Oscillo et Bécher), on peut vérifier la valeur de \(x_{C}\) en n'oubliant pas de régler convenablement les paramètres (Dans notre exemple, \(\alpha = 35^{o}\), \(v_{0}\) = 14 \(m.s^{-1}\), h = 2 m)

Flèche de la trajectoire
- Refaire une simulation en cliquant "Mouvement lent" et "Vitesse"
afin de voir l'allure du vitesse \(\overrightarrow{v_{S}}\) à l'apogée (sommet S)
de sa trajectoire ?
- Aide pour la question suivante : Que dire de \(v_{zS}\) ?
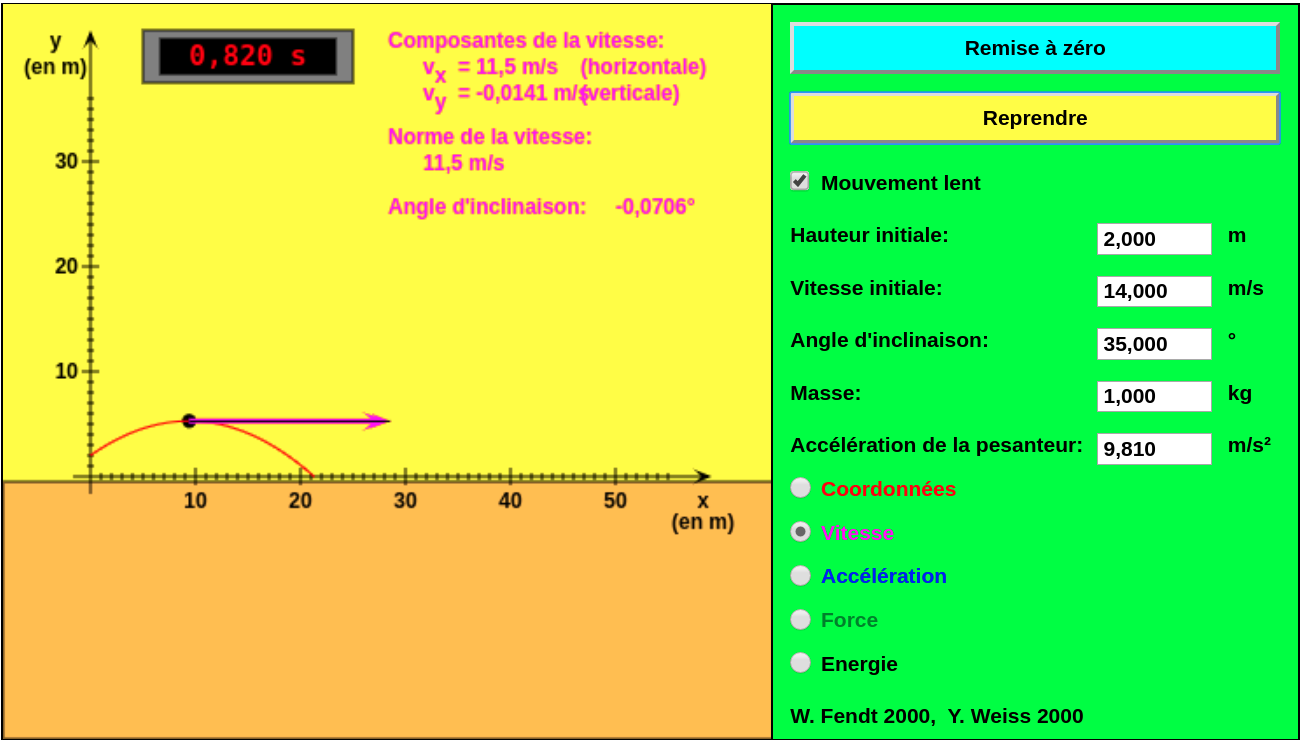
On remarque qu'à l'apogée, au sommet S, \(v_{zS}\) = 0 \(m.s^{-1}\)
- Quelle équation horaire ((1) à (9)) permet alors de trouver \(t_{S}\), temps qu'il faut au "poids" pour atteindre l'apogée (sommet S) de sa trajectoire ? Exprimer \(t_{S}\).
- L'équation (6) \(v_{z} = -gt + v_{0}sin \alpha\) donne, pour S,
\(v_{zS} = -gt_{S} + v_{0}sin \alpha = 0\)
- \(t_{S} = \frac{v_{0}sin \alpha}{g}\)
- Connaissant l'expression de \(t_{S}\), quelle équation horaire ((1) à (9)) permet de trouver la hauteur maximale \(y_{S}\) atteinte par le "poids" ?
- En remplaçant t par l'expression de \(t_{S}\), l'équation horaire (9) \(z = -\frac{1}{2} gt^{2} + v_{0}sin \alpha t + h\) permettra d'obtenir \(z_{S}\)
- \(z_{S} = -\frac{1}{2} g(\frac{v_{0}sin \alpha}{g})^{2} + v_{0}sin \alpha \times \frac{v_{0}sin \alpha}{g} + h\)
- \(z_{S} = -(\frac{v_{0}^{2}sin^{2} \alpha}{2g}) + \frac{v_{0}^{2}sin^{2} \alpha}{g} + h\)
- \(z_{S} = \frac{v_{0}^{2}sin^{2} \alpha}{2g} + h\)
- \(z_{S}\) est parfois nommée "flèche de la trajectoire"
- Dans notre exemple, \(z_{S} = \frac{14^{2}sin^{2}(35^{o})}{2 \times 9,81} + 2\) = 5,29 m
- On peut vérifier la valeur de \(z_{S}\) dans la simulation.
Durée \(t_{C}\) de la chute
- Quelle équation horaire ((1) à (9)) permet de trouver la durée \(t_{C}\) de la chute également donnée dans la simulation ?
Solution indépendante des précédentes
- Utilisons l'équation horaire (9) \(z = -\frac{1}{2} gt^{2} + v_{0}sin \alpha t + h\)
- Elle donne pour le point C : \(z_{C} = -\frac{1}{2} gt_{C}^{2} + v_{0}sin \alpha t_{C} + h = 0\)
- \(-\frac{9.81}{2}t_{C}^{2} + 14 \times sin(35^{o})\times t_{C} + 2 = 0\)
- \(-4,91t_{C}^{2} + 8,03t_{C} + 2 = 0\)
- L'équation du second degré précédente du type \(ax^{2} +bx + c = 0\) a deux solutions : Voir, par exemple, Résolution d'équation du 2d degré en ligne avec a = -4,91 ; b = 8,03 et c = 2.
- Ces solutions sont -0,220 et 1,86. La seule solution physiquement acceptable est bien sûr \(t_{C}\) = 1,86 s.
- On peut vérifier la valeur de \(t_{C}\) dans la simulation.
Solution utilisant \(x_{C}\)
- D'après (7) \(t = \frac{x}{v_{0}cos \alpha}\) d'où \(t_{C} = \frac{x_{C}}{v_{0}cos \alpha}\) = \(\frac{21,3}{14 \times cos(35^{o})}\) = 1,86 s.
