PYTHON POUR TRAITER DES DONNÉES (3)
Étude de la variabilité du volume mesuré par une pièce de verrerie
Table des matières
Pour une plus grande pécision possible, quelle verrerie choisir ?
Tests du bécher et de la fiole jaugée
RÉALISER
- a. Peser le bécher vide et sec : Noter la valeur de sa masse \(m_{1}\).
- b. Remplir d’eau déminéralisée jusqu’à la graduation 100 mL.
- c. Peser de nouveau le bécher avec l’eau, en déduire la masse mVb du volume d’eau mesurée dans le bécher.
- d. Peser la fiole jaugée vide et sèche : Noter la valeur de sa masse \(m_{2}\).
- e. Remplir d’eau déminéralisée jusqu’au trait de jauge à 100 mL (Voir document 4).
- f. Peser de nouveau la fiole jaugée avec l’eau, en déduire la masse mVf du volume d’eau mesurée dans la fiole jaugée.
- Quelle est la masse \(m_{theo}\) de 100 mL d’eau de masse volumique \(\rho\) = 1,00 \(g.mL^{-1}\) ?
On présentera les résultats collectifs dans le tableau suivant :
N° équipe 1 2 3 4 5 6 7 mVb (en g) mVf (en g)
ANALYSER
- Comment pourrions-nous illustrer la dispersion des résultats concernant les mesures de mVb et mVf ? Comment faire ?
- Choisir en justifiant qui du bécher ou de la fiole jaugée se révèle le plus précis pour mesurer un volume de liquide.
Utilisation du langage Python pour le traitement des données
Code source : Histogramme illustrant la dispersion des valeurs mVb et mVf obtenues par chaque équipe
import numpy as np import matplotlib.pyplot as plt plt.style.use('seaborn-deep') mVb=[96.4,93.42,102.9,96.66,92.25,92.34,96.51,95.06,97.07,97.81,96.97,94.53,100.64,97,97,103.17,93.16,92.08] mVf=[99.64,103.06,102.8,99.69,99.67,99.052,99.1,99.73,97.47,100.8,100.05,99.61,99.82,99,99,99.46,103.24,99.4] plt.hist([mVb, mVf], bins=10, label=['Bécher mVb', 'Fiole jaugée mVf']) plt.legend(loc='upper left') plt.show()
- On pourra faire un copier-coller du programme précédent vers un éditeur python en ligne comme …
- Vérifier que la compilation donne :
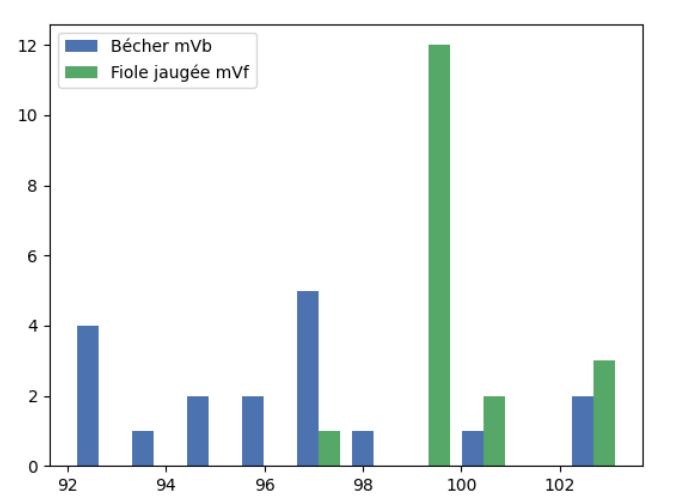
- Analyser l’histogramme obtenu.
Code source : Détermination de la moyenne, de l’écart-type et de l’incertitude échantillon d’une série de mesures
import math import statistics from statistics import stdev Vb=[96.4,93.42,102.9,96.66,92.25,92.34,96.51,95.06,97.07,97.81,96.97,94.53,100.64,97,97,103.17,93.16,92.08] print('Moyenne des mesures avec le bécher :') moyenneVb=statistics.mean(Vb) print(moyenneVb) print('Écart-type des mesures avec le bécher :') ecartypeVb=stdev(Vb) print(ecartypeVb) N=len(Vb) print('Incertitude-type des mesures avec le bécher :') incertitudetypeVb=ecartypeVb/math.sqrt(N) print(incertitudetypeVb) Vf=[99.64,103.06,102.8,99.69,99.67,99.052,99.1,99.73,97.47,100.8,100.05,99.61,99.82,99,99,99.46,103.24,99.4] print('Moyenne des mesures avec la fiole jaugée :') moyenneVf=statistics.mean(Vf) print(moyenneVf) print('Écart-type des mesures avec la fiole jaugée :') ecartypeVf=stdev(Vf) print(ecartypeVf) N=len(Vf) print('Incertitude-type des mesures avec la fiole jaugée :') incertitudetypeVf=ecartypeVf/math.sqrt(N) print(incertitudetypeVf)
- On pourra faire un copier-coller du programme précédent vers un éditeur python en ligne comme …
- Vérifier que la compilation donne :

- D’après les résultats, interpréter les écritures finales suivantes :
Mesure d’un volume d’eau V = 100 mL à l’aide d’un bécher :
\(V_{b}\) = 96,4 \(\pm\) 0,8 mL
Mesure d’un volume d’eau V = 100,0 mL à l’aide d’une fiole jaugée de 100,0 mL :
\(V_{f}\) = 100,0 \(\pm\) 0,4 mL
